A comparison of inexpensive, molded plastic lenses and their relative "accuracy" and ability to produce collimated beams.
Using Fresnel lenses for optical communications
Because of their low cost, low weight and availability in large sizes, Fresnel lenses are attractive options when used for optical communications. Being generally equivalent to PCX (Plano-Convex) lenses, they can be used for collimating beams of light as well as intercepting and focusing light from a distant source onto an optical detector.
Because such use isn't really what the designers of the Fresnel lenses had in mind, the question comes arises as to how "good" they are for such purposes? This is what we hope that this page at least partially answers.
What's a Fresnel lens?
 |
At around 1818 Augustin-Jean Fresnel used this realization to construct what is believed to be the first practical version of such a lens and it found immediate use in lighthouses owing to its ability to effectively collect and concentrate a significant portion of the lamp's overall light output and direct it as a tight beam. By being able to simultaneously collect much of the "wasted" light from the flame being emitted in other directions while minimizing the divergence of the resulting beam, this "Fresnel Lens" was able to increase the distance over which a lighthouse's beam could be seen essentially to that of line-of-sight.
As can be seen from Figure 1 the Fresnel Lens's primary advantage is that its weight and thickness can be greatly reduced by utilizing only those portions of the lens that actually contribute to the "bending" of the light's rays. In its original primary application - lighthouses - the fact that the lens was broken up into smaller "facets" was of little importance, even though such a lens wasn't particularly useful for imaging purposes such as telescopes. What it is good at is concentrating light (such as from the sun) onto a small area or at producing reasonably well-collimated beams from light sources.
Fresnel lenses are typically made to be equivalent to an aspherical lens - a property allows them to properly focus light with minimum spherical aberration - even with a small F-number. By making a large lens with a very short focal length (hence, a small F-number) the entire lens/lamp assembly could be made to be reasonably small and light - an important consideration if it was to be used in a lighthouse and rotated about the source!
Another excellent reference on this topic is Fresnel Technology's brochure, Fresnel Lenses - link to .PDF.
Limitations of Fresnel lenses
Even though lighthouses are relatively rare, Fresnel lenses are now quite commonplace. Their main attraction is that they can now be made rather inexpensively, the shape of the lens being molded using plastic and can be found in products as diverse as projection televisions, infrared intrusion detectors and photographic flash units. With modern techniques it is now possible to shrink the size of the facets such that even a large, "strong" lens can be made to be only a few millimeters thick.
Despite modern manufacturing techniques and materials Fresnel lenses are still inferior to "conventional" lenses when it comes to being able to produce high-resolution images - and for several reasons:
- Material stability. Being stamped into thin material, it is important that it be kept flat. Without much intrinsic strength, distortions, bowing and warping are inevitable in lenses made from thin plastic.
- Precision. During manufacture, thermal expansion/contraction of the plastic can complicate precise replication. Slight variations of the mechanical and optical properties of the plastic stock used to manufacture lens can also result in slight differences between batches of seemingly-identical lenses.
- Resolution. Because the lens contains individual facets, the transition between these individual facets cause a slight "discontinuity" in the optical properties of the lens: The smaller the individual facets are, the more-closely it can (in theory) resemble a conventional lens and improve its optical quality, making the individual facets harder to see. It is only practical to shrink the size of the facts by a certain amount before the aspects of their individual shapes become difficult to replicate accurately on a small scale.
- Scattering. Because a Fresnel lens consists
of discontinuities between the individual facets, these
"steps" tend to cause some scattering - particularly of
off-axis light. In general, the smaller the facets,
the worse this problem becomes.
- Imaging. They aren't very good at being able
to focus an image to fine detail. It is for this
reason that you are unlikely to see Fresnel lenses used on
telescopes and cameras! In addition to this, chromatic
aberration (e.g. "color fringing") is an issue with
such a lens, particularly at lower f/D ratios.
- Not diffraction-limited. One of the limits of precision of an optical system is related to the fact that the wavelength of light - although very small - is, in fact, finite. It is this fact that imposes the absolute limit as to how fine-focused rays of light may be - even if the lens is "perfect." If a lens is accurate enough that its imperfections contribute less to image degradation than the wavelength of light we refer to that lens as being "diffraction limited". Owing to the practical construction constraints of mass-produced Fresnel lenses, it is unreasonable to expect performance that approaches diffraction-limited optics as the methods and materials are not accurate enough to achieve and hold such accuracy.
- Coherent light. Because of they aren't likely to be accurate enough to reach the diffraction limit, Fresnel lenses cannot be used to efficiently and cleanly collimate a coherent light source such as a laser and attempts to do so can result in a significant portion of the light being scattered. It is worth mentioning that after a laser passes even a short distance through the atmosphere (a few kilometers will do it!) it loses enough of its properties of coherence so that you can use Fresnel lenses to focus the "formerly coherent" light from a laser onto a detector at the "receive" end.
| F-number |
Approximate
diameter
of
the "Airy Disc" |
| 0.5 |
0.00038mm |
| 0.75 |
0.00058mm |
| 1.0 |
0.00077mm |
| 1.25 |
0.00096mm |
| 1.5 |
0.0012mm |
| 1.75 |
0.0013mm |
| 2.0 |
0.0015mm |
| 2.5 |
0.0019mm |
| 3.0 |
0.0023mm |
| 5.6 |
0.0043mm |
| 11 |
0.0085mm |
| 16 |
0.0123mm |
| 22 |
0.0169mm |
| 50 |
0.0384mm |
| 100 |
0.0769mm |
| 200 |
0.1537mm |
How good are "ideal" lenses?
At this point, the question of "How good would a perfect lens be?" comes to mind.
As mentioned above, one should ideally be able to focus a light source (such a star) that is, for all practical purposes, infinitely distant (and hence its rays parallel) to an absolute point. Diffraction prevents this from happening, resulting in what is referred to as an Airy Disc - a fuzzy spot that represents the minimum size attainable at that wavelength in a lens system - this being due to the fact that light waves - while very small - are not infinitesimally small!
Assuming a monochromatic light source with a wavelength of 630nm, Table 1 shows the calculated airy disc size for several representative F-numbers (a.k.a. the "F-ratio" or "f/D" radio, the diameter of the lens divided by its focal length - the terms being used interchangeably) of "perfect" lenses at that wavelength. Observe that the theoretical size of the airy disc is not related to the size of the lens - just the F-number!
The equation for the approximate size of the airy disc is:
f is the focal length of the lens being evaluatedSo, how close are typical Fresnel lenses to achieving performance near that of the Airy disc? That's what we hope to answer.
d is the diameter of the lens being evaluated
λ is the wavelength of light
x is the diameter of the airy disc in the same units of measurement as f, d and λ
(Note that the quantity f/d is the F-number!)
Types of Fresnel lenses commonly available to the amateur experimenter:
There are a number of different types of Fresnel lenses available to the experimenter, but only those that are made of plastic and can be obtained at reasonable cost either on the new or surplus market will be discussed here. The vast majority of Fresnel lenses that are available are equivalent to a Plano-Convex (PCX) lens as depicted in Figure 1. A trait common to these lenses is that they are oriented "grooves-out" - that is, the grooves face the distant object while the flat side faces the light source (or detector.)
First a warning about all Fresnel lenses!
PLEASE READ the warning to the right concerning Fresnel Lens safety!
Once you have read it, read it again!
|
A few words about
Fresnel lens safety
Fresnel lenses can be dangerous! You should always treat a Fresnel lens with respect - as if it were an open flame! If you consider that a small magnifying glass and direct sunlight can burn paper, it is not surprising that even a rather small Fresnel lens (20x28cm) can concentrate enough sunlight to instantly incinerate paper, burn wood and even vitrify some types of sand! When experimenting with a Fresnel lens, always treat it as if it were an open flame - and children should not play with it unless they are supervised! Even the briefest exposure of skin at the focal point of a Fresnel lens exposed to full sunlight can instantly cause severe burns! If you store a Fresnel lens, you should always do so in such a way that it can never be exposed to sunlight! If, for example, you left a Fresnel lens in a location where, at some time of day, it was exposed to the sun and there was something on the other side of the lens at even approximately the focal length of that lens, it could be burned when the sun angle was appropriate. If you mount a Fresnel lens in a frame, make sure that it is stored such that it can never be exposed to sunlight. If you are transporting such a lens, always carry it in a covered box or drape it with cloth to prevent it from being exposed to the full and concentrated energy of the sun! In other words, an improperly-treated Fresnel lens can not only burn you, but it can case severe property damage! |
"Giant" Fresnel lenses
These lenses often appear on the surplus market, many of which were made for cathode-ray ("tube type") big screen televisions but are often sold as "fire starters" or solar ovens. Typically made using flexible optical plastic, many of these lenses measure around 1 meter diagonally. To use these lenses effectively they must be mounted in a rigid frame as it is imperative that they remain as flat as possible in order to accurately focus. In other words, you cannot "hand-hold" them and expect any reasonable performance - they must be mounted in a frame!
Because they were used for imaging purposes they have quite fine "groove" pitch (that is, small facet size) - typically on the order of 0.2mm. This fine pitch also means that they tend to scatter a fair amount of off-axis light as there are plenty of facets to do the scattering in the first place. The grooves on these fine-pitched lenses are quite fragile and tend to accumulate dust, further reducing their efficiency and increasing scattering.
While the light-gathering capabilities of these lenses are impressive, the main disadvantage of these types of lenses is, in fact, their size. They are difficult to transport, rather fragile, and if used outdoors they tend to act like a sail and catch every bit of wind - something that makes holding a precise aim very difficult! Finally, because of their light-gathering capability, they are even more potentially-dangerous than smaller Fresnel lenses!
"Page magnifier" lenses
Another source of Fresnel lenses that should not be overlooked are the inexpensive lenses often found at office supply and stationary stores that are approximately the size of an A or A4 sheet of paper - 20x28cm or so. These are intended to be used for magnifying entire pages of text at once and to aid in reading maps and even though their optical quality isn't extremely high, they do quite a good job.
These "page magnifiers" can be found for anywhere from $1-$15 each - but if you see one for more than $5, keep looking for a better price!
These lenses are available in two different styles:
- Flexible lenses. Stamped in clear vinyl, these are flexible and are usually mounted in some sort of flexible plastic frame to allow them to be kept in a 3-ring binder.
- Rigid lenses. These appear to be stamped in
clear acrylic or similar. Optically, they are
generally equivalent to flexible types, but are quite rigid
and are not intended to be bent.
The rigid lenses have the obvious advantage that could be mounted in a box directly, without a frame, but it is very important that they are not inadvertently warped when being mounted or being subject to the normal stresses of the box. Even though they are rigid it is worth considering using a pane of glass in a frame - or at least a sheet of clear plastic (such as that used to make replacement windows) - as not only will this protect the fragile "grooved" side of the Fresnel from accumulating dust and dirt but it will also reduce the likelihood that it will be accidentally damaged in handling. Another advantage of using a frame with a pane of glass or clear plastic is that this will help to relieve the Fresnel itself from the stresses of the box being used to mount the lens that could cause the plastic lens to be warped and degrade its optical performance.
As will be demonstrated below, the while both are suitable for their intended task, the optical quality of the "rigid" lenses if much higher than that of the "flexible" lenses.
The "magnification factor" on the package means nothing!
It is common for these page magnifier lenses to boast ratings in "powers of magnification" - usually "2x" or "3x". In reality, these numbers are meaningless as they don't have much bearing on what you really want to know - and that's the focal length.
We've noted that these page magnifier lenses seem to come in two general ranges of focal lengths: In the 30cm range and in the 60cm range - give or take a few of centimeters. For practical reasons, which will be discussed later, you should choose page magnifiers that have a focal length that is 1-1.5 times the "long" dimension (e.g. the length) of the lens that you use which, in this case, would indicate the use a lens with a focal length in the general area of 30-35cm.
Typically, these page magnifier lenses are packaged with a plastic window such that the potential buyer can test them prior to purchase and this lends nicely to being able to determine the focal length in the store, before you buy them. To check their focal length, simply hold the lens up and focus the lens onto a piece of paper, measuring the distance between the lens and the paper, but when you do this make sure that the grooved side is pointed away from the paper and that you pick as distant an object to focus as you can: If the store has windows, try to focus the scene outside using a distant object. Note that sometimes these lenses are sold as pairs with two in a package and unless you can test just one of these lenses at a time (which would probably mean opening the package) the above test won't work!
Overhead projector lenses are usually terrible!
One potential source of Fresnel lenses for experimenters have been overhead projectors. Typically, these lenses are built into the plate onto which the transparency is laid, with the Fresnel lens being used to direct the light upwards toward the right-angle mirror or lens assembly and onto the screen.
Unfortunately, these lenses are NOT usually suitable for purposes of collimation or the focusing of a distant light source onto a detector as they may not be designed to focus at infinity. Since their main purpose is usually that of concentrating the light from the projection bulb and not forming an image directly, they do not function as needed and often blur and/or scatter light should they be attempted to be used.
"Computer Monitor Enhancement" lenses
One possible source of Fresnel lenses are those sold to enhance the computer-gaming experience. By placing a Fresnel lens in front of a computer monitor one can achieve the illusion of a much larger monitor and field of view than is actually present. These types of lenses are often somewhat larger in size and with smaller facets (to improve image quality) than those of page magnifier lenses and some of the lenses sold by 3dlens.com (including lens #1, the "F550" tested below) are marketed for such purposes.
Special-purpose lenses
There are a number of suppliers that specialize in Fresnel lenses and some of them are of very high quality. Unfortunately, when purchased new, these lenses can be quite expensive compared to the inexpensive page-magnifier types - that is $30-$100 as compared to $1-$15 for a comparable-sized page magnifier. Occasionally, these high-quality lenses show up on the surplus market, but these sources tend to be intermittent and you must be certain that you know exactly what you are getting!
As with traditional glass lenses, Fresnel lenses can be made to have both positive and negative focal lengths and have a variety different optical properties. If you wish to buy a lens for optical communications it is recommended that it be as square as possible, optically equivalent to a plano-convex lens (and therefore have a positive focal length) - preferably with the grooves facing outwards, designed for being focused to infinity, have an F-number of around 1, and be made from optical acrylic or a similar material.
For a partial list of sources of various types of lenses, see the "Optical Sources" page at this web site.
"Grooves out" versus "Grooves in"
Most commonly-available Fresnel lenses are "Positive" lenses that function as a Plano-Convex lens as depicted in Figure 1, above. While many different configurations are possible most of these lenses are made so that the grooved side goes toward infinity - that is, the "grooved side" goes away from the LED or detector.
In the unlikely event that you find a "Grooves in" (that is, the "grooved" side goes toward the LED) type of lens, this property can be readily demonstrated by focusing a distant outdoor scene onto a white piece of paper or wall. If one tries the lens both ways (e.g. grooves out and grooves in) the "proper" orientation will be apparent with an image that is sharper and/or brighter than can be had when the lens is oriented the "wrong" way!
Note that in a casual test it may seem that a Fresnel lens may focus well either grooves-out (toward infinity) or grooves in, but a careful examination will reveal that this is not the case: The proper orientation can be determined simply by focusing an outdoor scene (through a window) onto a white sheet of paper or a wall and noting that one direction provides a better (sharper image, improved contrast) than the other way: A nighttime scene with points of light (e.g. streetlights) is helpful in that an improperly-oriented lens can cause fuzzy halos to appear.
Practical optical systems using Fresnel lenses
For practical reasons, it is recommended that an optical system using Fresnel lenses be designed using lenses that have an F-number in the range of 0.5 to 1.5 - that is, around 1. Remember: The "F-number" is the focal length divided by the diameter of the lens, so for an F-number of unity or one, the "diameter" of the lens would be approximately the same as its focal length.
|
What's the "diameter" of a
square or rectangular lens?
Most Fresnel lenses aren't round! Because the F-number is the ratio of the focal length divided by the diameter of the lens, how do we express the "F-number" of a "non-round" lens? For the purposes of this web site, the F-number is generally based on the "wide" dimension of a rectangular lens - but not from corner-to-corner. So, if we had a lens that had a "grooved area" of 268mm by 200mm with a 330mm focal length, we'd generally say that the F-number was 1.23. |
Why the recommendation of this F-number range?
The main consideration is that of practicality. Consider a hypothetical lens with a diameter of 30cm. With an F-number of 1, the focal length will also be 30cm, and if you were to construct a box that contained both the lens and, say, a detector at the focal plane, it would be about 30cm in length. From a practical standpoint such a box (which would be roughly cube-shaped) would be of a manageable size and wouldn't be too difficult to handle.
Consider, then, a similar lens with an F-number of 5. If we take this same lens - one 30cm in diameter - we will have to place the detector of our hypothetical box 150cm (nearly 6 feet!) away from the lens: It is easy to see that such a structure rapidly becomes quite large and cumbersome, requiring a lot of material and it would be difficult to transport!
Because Fresnel lenses aren't constrained in their design in the same way that traditional lenses might be it is perfectly reasonable to construct a Fresnel lens with an F-number of unity: Indeed, Fresnel lenses are commonly available with F-numbers from 0.5 to 4 or so. From a practical standpoint, most inexpensive Fresnel lenses are made to have F-numbers in the range of unity to 2: Too-small an F-number and one runs into practical considerations related to the refractive index of the material used for the lens as well as the geometry of the facets, while a higher F-number implies increasingly-greater precision of the lens and its dimensions in order to maintain a precise focus - both being factors that translate to greater cost in manufacture
Another reason for the recommendation of this F-number range relates to using the lens in an optical transmit/receive system and this could be the basis of an article it its own right, so only a few of the details will be discussed here. For transmitting this has to do with being able to efficiently couple the light from the LED to the Fresnel itself - usually through the use of a "secondary" lens being used to narrow the beam of light to "illuminate" the back of the Fresnel. If the F-number is larger - above about 1.5 - this becomes increasingly difficult to do with a simple secondary lens system owing to the need to use an increasingly "stronger" (smaller F-number) secondary lens next to the LED as the F-number of the Fresnel lens system increases: At some point the F-number of the required single secondary lens gets too small to be practical.
At the other extreme (e.g. smaller F- numbers - in the area of 0.5) the problem becomes largely one of geometry. One problem that such an F-number implies is that a wide illumination angle is required from the perspective of the emitter and this means that the edges of the lens are significantly more-distant from the emitter than the center of the lens. This difference in LED/Fresnel distance increases the amount of "falloff" in the amount of light that gets to the edges of the lens, potentially making the system less efficient. For reception, it's also worth noting that the responsiveness of many detectors decreases when the incident light arrives at angles far-removed from the center axis.
Fresnel Lenses for through-the-air optical communications
Transmission and collimation:
It is also possible to use a Fresnel lens as a collimator - that is, an optical system to produce highly-parallel beams like those of a spotlight as seen in Diagram 2. As noted before, the imprecise nature of a Fresnel lens precludes their efficient use to efficiently collimate coherent light (such as that from a laser) as an inexpensive, molded Fresnel lens may not practically be made to be accurate enough to be diffraction-limited. In other words, attempts to use a Fresnel lens for laser light will likely result in a significant percentage of that light being scattered rather than being collimated.
As readers of this, the modulatedlight.org site, are already aware, we extensively discuss the use of non-coherent light sources (such as LEDs) in optical communications systems and Fresnel lenses are nicely suited for that purpose!
The "ideal" shape of a Fresnel lens would be one that is round as this would match the shape of the circle of light that is typically emitted from an LED/secondary lens emitter assembly. Departures from this "round" shape imply a loss of light owing to some portion of that circular "pool of light" being projected onto the backside of the lens being cut off along the edges with this loss of efficiency becoming even worse as the lens is made more-strongly rectangular. Since it is rather rare to find a large, round Fresnel lens on the surplus market - and due to practical difficulties in mounting a round lens - square or rectangular lenses are, by far, the most common. It's worth mentioning that the shape of the lens is not particularly important when used for receiving as the shape of the spot of light being focused onto the detector has little to do with the aspect ratio of the lens.
As previously noted, when using an LED (or other light source) with a Fresnel lens it is generally necessary to use a secondary lens (between the emitter and the Fresnel) to match the beam characteristics of the emitter to the apparent subtended angle of the Fresnel as "seen" from the viewpoint of emitter assembly. While adding this lens necessarily increases the apparent size of the emitter, the loss of efficiency due to the subsequent increase of divergence is usually much more than offset by the increased overall efficiency of the system as a whole. Unfortunately, a more in-depth discussion of this topic is beyond the scope of this page but can be discussed with the author via email.
Reception and detection:
For optical communications it is desirable to use a large an aperture lens as practical to intercept as much energy as possible from the distant light source. In addition to intercepting this energy it is also desirable that the field of view be reduced in order to reject off-axis light sources that could degrade the communications link.
The question arises, then: "How good is a typical molded Fresnel lens?"
Again, while not generally suitable for imaging, analysis of the quality of the image produced by these lenses when observing a point source of light can be instructive in determining a few qualities of its construction - namely the accuracy of the facets comprising the lens. For optical communications purposes where radiometric detection is employed - that is, energy from the distant source is detected, generally irrespective of its specific wavelength - light from the distant source is focused onto the active area of the detector, producing an electric signal that is then amplified.
It makes sense, then, that it is desirable that as much of the light being intercepted by the lens gets focused onto the detector and that as little as possible of this light is wasted by "missing" the detector. To accomplish this a "minimum" size of detector is implied - that is, if the area of the detector is much smaller than the spot produced by the lens when it is optimally focused, then not all of the light from the distant source will strike the detector and contribute to its detection resulting in unnecessary loss of detection efficiency.
Conversely, if the detector is too large, there are two potential problems: A larger detector implies a wider field of view which means that it is likely that stray energy from other sources of light that are off-axis may fall across the detector, possibly "diluting" the desired signal source. The other problem is that a larger detector (particularly a photodiode) can have worse sensitivity than a smaller diode as the larger device will likely have a higher capacitance and higher intrinsic noise than a small one. In other words, it's not usually beneficial to have a diode so large that only a small portion of its active area gets illuminated by the distant light source!
Note: A large aperture lens also reduces the effects of scintillation of the detected signal due, in part, to the fact that a larger lens offers a degree of spatial diversity. A large lens also minimizes effects of "local coherence" - another potential contributor to scintillation.
Efficiency:
Another question that arises in this discussion is: How efficient is an optical system using a Fresnel Lens as compared with one of equal size using glass lenses? This is a difficult question to answer and the estimates that I have seen seem to vary.
High-grade optical acrylic can have very low transmission loss at the design wavelength - roughly comparable to glass. Considering that far less material would be used in a Fresnel lens than a "conventional" glass lens of similar optical properties (e.g. the Fresnel would be much thinner) there is less material contained within the Fresnel to contribute to losses.
Another factor having to do with efficiency is the fact that a Fresnel lens consists of a number of facets. At their transition points, some degree of loss (largely through scattering) occurs due to these facets - the problem being arguably worse with increasingly-fine "groove pitch" lenses, not to mention the accuracy and "sharpness" of these facets.
Finally, there is the issue of accuracy of the lens itself. Since a Fresnel lens cannot achieve the precision of a high-quality glass lens it is safe to assume that it cannot focus nor collimate a beam as tightly as an ideal lens. This, however, does not actually affect the light-gathering ability directly as if one uses a suitably-large detector, all of the light from the distant source can still be intercepted - albeit over a larger focused area. What it does affect is the minimum field of view (in the case of the detector) and divergence (in the case of the emitter) of the system - both being factors that can affect the performance of the system to a degree but not necessarily its absolute ability to gather/emit light.
If we were to assume that a Fresnel-based system were only 50% efficient as compared to a similar-sized glass lens (a number that is likely pessimistic with high-quality Fresnel lenses) it should be remembered that this deficiency could be compensated by using a Fresnel lens that was 1.4 times the diameter (hence twice the area) of the glass lens. Because of their light weight and low cost, constructing a receiver that used a larger Fresnel lens to make up this difference would be quite practical while in the case of the transmitter, the larger exit aperture would be of benefit in minimizing the effects of scintillation and could, to some extent, reduce divergence.
Divergence:
When used with an emitter it is desirable that the divergence be minimized in order to achieve the highest-possible far-field flux (brightest light) at the greatest distance. As with any type of lens or reflector, the amount of divergence is related to the inverse ratio of the area of the emitter versus the area of the lens being used to collimate. In other words, the tiniest emitter plus the largest lens will result in the lowest amount of divergence!
In a laser pointer, good collimation occurs because the laser's emitting area is only a few 10's of microns across. This, coupled with the fact that the lens is going to be a few millimeters in diameter implies a pretty good "lens/emitter" area ratio. In an LED-based system, a typical high-power LED can be millimeters in size so it's not too surprising to note that an extremely high "lens/emitter" ratio would imply a large Fresnel lens, indeed! As will be demonstrated below, the divergence of a lens system using Fresnels is probably going to be set by the actual size of the emitter itself rather than the quality of the lens!
What can we learn by knowing the size of the "blur circle?"
Because a Fresnel lens is unlikely to approach the diffraction limit at visible wavelengths it would be improper to refer to the minimum "spot" size produced by such a lens as an "airy disc" - that is, a pattern resulting from the wave properties of the light itself. To describe the smallest "spot" of light that we get with an "imperfect" lens we'll use the phrase "blur circle" - a term akin to the "circle of confusion".
What, then, can we determine by analyzing the lens's blur circle?
- How good is the lens? The relative size of the blur circle from an optimally-focused lens resulting from a distant light source can tell us something about the quality of the lens being tested.
- What is the minimum recommended size of the detector? By knowing the area over which the light can be focused can tell us something about the size of detector we would use.
- Is the divergence of the
collimated beam set by the size of the emitter, or the
quality of the lens? In any collimated system
the divergence is set, at least in part, by the ratio of the
aperture size and the apparent size of the emitter. If
the surface area of the emitter being used is somewhat
larger than the blur circle, one can be reasonably sure that
the divergence of an optimally-focused collimator system
will be set primarily by the size of the emitter rather than
the quality of the lens. Conversely, if the emitter's
area is much smaller than the blur circle, it is
likely to be the quality of the lens that will dictate the
system's divergence.
Methods of determination the size of the blur circle:
Determining the number of pixels per millimeter:
Fortunately, it is practical to measure sub-millimeter spot sizes with reasonable accuracy. Using a digital imager of known dimensions it is possible to ascertain the approximate dimensions of a the blur circle by analyzing the resulting picture. For this I used a high-sensitivity "CS mount" CCTV video camera with its lens removed and a video capture device on a laptop computer. With this setup, real-time images can be displayed on the computer's screen while the Fresnel-to-imager distance and angles are adjusted for optimal focusing and planar alignment, projecting the image from the lens directly onto the imager. Once the adjustments are made, the image is then digitized and notations made for later analysis. When making final measurements, remember that it's the size of the final image after digitization and not the actual resolution of the imager that should be considered when calculating the number of pixels per millimeter. When using an analog video camera and digitizing the result it's usually the case that the resolution of the captured image doesn't exactly match the resolution of the imager!
For some cameras determining the actual size of the imager's "active area" and from there, the size of the pixels, can be difficult as described in the article, "Making (some) sense out of sensor sizes." Fortunately, with CCTV cameras intended for use with standard "CS" (or "C" mount) lenses, the "size" of the sensor is typically spelled out in the camera's specifications and from that it is possible to work backwards and determine the number of pixels per millimeter of the imager. For example, for a standard "1/2" CCTV imager the active area is typically 6.8mm x 4.8mm and from this, it is possible to estimate the pixel size of the resulting image.
If a DSLR with a removable lens or a modified webcam is used instead of a CCTV-type camera you are on your own to determine - as best you can - the physical dimensions of the imager's active area and thus the image's pixel's "pitch." Finally, be aware that not all cameras/digitizers produce "square" pixels.
Source of light - Star:
In order to properly test a lens that is to be used for collimation or detection, an infinitely-distant, point-source is ideal as an light source as it would push a "perfect" lens to its diffraction limit. Assuming that the pixel size of the imager is adequate to resolve the size of the blur circle of the Fresnel lens (an assumption that we'll make for the moment) that leaves us with the selection of the light source.
One group of possible light sources may be found in the night sky: Stars and planets. Stars definitely fit the bill when it comes to being adequately-distant, point-sources of light, but their use has several drawbacks:
- They are usable only during a clear, cloud-free night. This is obvious and isn't as much of an inconvenience if you live in a desert like I do, but it does limit when - and to some extent, where - testing can be done - that is, nighttime and not during winter!
- They usually "twinkle." Because of scintillation, the brightness (and, to some extent, the apparent position) of a star can vary randomly due to atmospheric effects. This can complicate measurements, as you might suspect!
- They aren't usually located at convenient elevations. It is more likely that a star will be located at a rather awkward angle in the sky. Practically speaking, it is preferable to have a light source either straight up (at the zenith) or on the horizon (which is unlikely!) as those locations make mounting and adjusting both the lens and camera most convenient.
- Stars are always "moving." Once you get everything lined up - which, itself, is not an easy task - the rotation of the earth will cause the star's apparent position to drift off. Clearly, this movement complicates setup of the lens and the subsequent capturing of an image.
- Starlight is not monochromatic. Because a Fresnel lens is a rather simple lens, it suffers from Chromatic Aberration which means that white light is separated into its constituent colors, spreading the image and making precise alignment (e.g. focusing) more difficult - a fact exacerbated by the short F-number of typical Fresnel lenses. Practically speaking, one can place a color filter in front of the imager and/or do some post-measurement image processing to remove certain colors to reduce this effect.
 |
Instead of stars, it is possible to use planets. Using a planet as a "point source" has the advantage that it can, depending on the planet and its distance, be much brighter than most stars, and its subtended angle is sufficiently large that it is less-likely to twinkle, but they are bright enough that one has to be careful to not saturate the imager being used and make precise adjustment and subsequent measurement difficult. Unfortunately - like stars - you need to constantly track them! Another consideration is that because of their large apparent "size" (owing to their relative nearness when compared to stars) they may not be small enough to sufficiently test the lens to its limits.
Using the above method and using the star Vega I was able to determine that the blur circles of the Fresnel lenses that I have are more than large enough to be discerned with a CCTV camera's imager - a fact that confirmed that it should be possible to make reasonably accurate measurements.
Source of light - Artificial:
Using a star and having determined that a CCTV imager had more than adequate resolution to measure a typical Fresnel lens, attention was paid to the possible use of an artificial light source for testing. Much more convenient than relying on a properly-positioned, moving star on a clear night, an artificial light source would allow repeatable measurements but the question was "How does one simulate an infinitely-distant point-source to adequately test the lens?"
As it turns out one doesn't need to have such a light source to test a Fresnel lens. Rather than being infinitely-distant (which would be very inconvenient!) a light source with a small subtended angle may be placed relatively close to the lens to adequately determine its "blur circle" properties. By producing one's own light source it is also possible to make it monochromatic (e.g. one color) to minimize chromatic aberration of the lens being evaluated as well as testing the lens at the wavelength for which operation is anticipated.
To produce a "spot source" of light I constructed the device shown in Figure 3. Using a 0.25mm drill bit, I made a hole in a 0.15mm thick piece of sheet brass. In a small, light-tight box made from double-sided printed circuit board material I enclosed a high-brightness red LED (a Liteon P/N: LTL912SEKSA, which is also a Radio Shack #276-020) and soldered to the box - covering a larger hole - the piece of brass with the 0.25mm hole which was aligned with the LED. Also contained within this box is a simple current regulator connected to a switch that allows either 60mA or 2mA of LED current to be selected: The high-current setting provides enough light, using a white piece of paper, to establish the aiming and rough focus of the Fresnel lens onto the camera's imager while the low-current setting prevents saturation of the camera's imager and makes final focus easier. This device also has 1/4"-20 threads tapped into a bottom hole to allow it to be attached to a standard tripod mount.
Even though the 0.25mm diameter spot of light is only about 15 meters away (hardly "infinitely distant"!) and the focus of the lens being tested is slightly "off" from what an infinitely-distant source would be, the results have been compared, using some of the same lenses, to those obtained using the star Vega and they seem to agree nicely indicating that this should be a reasonable method of ascertaining lens quality - especially since we are hardly likely to approach the diffraction limit with these lenses, anyway!
Methods that use lasers:
Before anyone else mentions it, I'll point out that I am aware of methods using lasers to test the focus and quality of lenses but I dismissed these methods for testing these lenses for a number of practical reasons: If you are already familiar with these methods then you'll appreciate the implied difficulty of testing large aperture plastic lenses with many facets!
|
The results
Important:
- When interpreting these results, the absolute brightness
of the images is less-important than the size and
shape. Because camera imagers are not linear, it is
not possible to make accurate determinations of absolute (or
relative) brightness.
- As can be seen, each image includes a scale to allow the
viewer to relate the image size to 1 millimeter, allowing an
estimation of the size of the spot. Note that the size
estimations are somewhat subjective and approximate.
- Noted in each of the descriptions is the approximate "F-number" of the lens. Because most of the lenses are rectangular rather than being round or square, the F-number given is always based on the long dimension of the lens. This is done because, when used as a collimator, it is generally best to treat the lens as if it were round with the diameter approximately equal to the long dimension. The reasons for that are beyond the scope of this page, but if you want to know you can always drop an email to the address linked at the bottom of this page.
Comment: In theory, it should be possible to
"re-linearize" the brightness (to compensate for the
intrinsic "gamma" of the camera) of the pixels in the
resulting images and make an estimation of the amount of
light energy contained in a particular unit-area of the
spot. This could be used to determine, with reasonable
accuracy, the various sizes/areas in which different
percentages of the total amount of energy, that the spot
contained.
 |
This lens is sold by 3dlens.com in Taiwan and is available via the internet, shipped by mail. This lens is constructed of optical acrylic, it is 320mm x 400mm, 2mm thick, has a "groove pitch" of 0.2mm, a focal length of 550mm and is approximately 2mm thick.
As can be seen from Figure 5 the vast majority of the light is concentrated into an area under 1mm diameter although some of it is scattered across a larger area. Visible in the picture is a slight amount of coma owing to the fact that distant light source was slightly higher than the center of the lens, but the image is "pretty close" to the optimal image obtained. (I should probably re-do this one someday.)
With an F-number of about 1.375 this lens is a bit on the "long" side of what I recommend.
Fresnel lenses with fine groove pitches (the 0.2mm pitch of this lens is considered to be fairly fine) tend to have greater scattering losses than "coarser" lenses owing to the greater number of facets over the surface of the lens. These scattering losses can decrease the rejection of off-axis light sources as well as somewhat increasing its transmission losses.
Compared to the other lenses tested, the performance of this lens was somewhat disappointing as the size of the blur circle is a bit larger than expected. Practically speaking, however, this lens would work well in a system using an LED of several square millimeters in size and a detector of the size of a BPW34.
|
Lens #2 - Surplus Shed L3606 (229mm F.L.):
The second lens was obtained from SurplusShed.com (P/N: L3606) and is 250mm x 318mm and is also made from optical acrylic about 2mm thick.
While the manufacturer of this lens is unknown, it appears to be of high quality but (unfortunately) their supply of this lens has been depleted. I ordered this model number of lens on two occasions and the first time, I received lens tested below (#10) - but after successfully using that lens in my first enclosure, I ordered some spares. Interestingly, the "new" lenses - although the same size and with the same part number, had a 100mm shorter focal length than the others - about 229mm.
As can be seen, the lens produces a spot that is significantly "denser" than that of lens #1 - a trait due, at least in part, to its much-shorter focal length. This lens has an F-number of about 0.72 which is short, but perfectly usable.
The groove pitch of this lens is "medium" at approximately 0.5mm which reduces scattering losses as compared to finer-pitched lenses.
Lens #3 - Rigid "Page Magnifier" from an office supply store:
The third lens is rather interesting: It is an inexpensive lens, sold as a "page magnifier" obtained from American Science and Surplus and was Stock #38939 (no longer available.) This lens is 213mm x 280mm, about 2mm thick with a clear "border" around its edges, resulting in "lens area" of about 268mm x 200mm. These types of lenses may also be found at office-supply and stationary stores and the occasional bargain shop or "dollar store" - or even online (e.g. Ebay, Amazon), often under the brand name of "Bazic" described as a "Full Page Magnifier" with "2x" magnification as part number 2708.
With a focal length of about 330mm, it has a moderate F-number of 1.23 (based on the "long" dimensions of the lens's "active" area) and a groove pitch of around 0.5mm. This image in Figure 7 is very slightly misfocused (which explains the dark spot in the center of the blur circle) but the size of the spot is correct.
As can be seen in Figure 7 this lens produces a nice, tightly-controlled spot of light due, at least in part, to its relatively small size (that is, there is "less" of the lens present to be inaccurate.) The performance of this lens - even though it is very inexpensive - is surprisingly good, especially considering that it was intended solely as a "full page magnifier" where significant optical distortion would not otherwise detract from its intended use.
Having had the opportunity of briefly examining several different types of these lenses I've noted that they are all about the same size (varying a few only a centimeter or so in each dimension), approximating a sheet of "A-size" (or "A4" size) paper with the exact dimensions depending on the supplier. We have noted that there are two distinct ranges of focal length: 300-350mm (usually in the 320-350mm area) and around 620mm - but it is only this lens (approximately 330mm F.L.) that I have had the opportunity to test!
It should be noted that the longer focal-length versions (around 620mm or 24") are not as useful for optical transmitters/receivers as the shorter focal-length lenses for several two main reasons:
- A 620mm focal length implies a fairly large structure - long enough to accommodate the lens and the electronics at the lens's focus. Such a box is large enough to be awkward to be constructed and transported.
- A large F-number of about 2.3 makes it very difficult to
efficiently couple the optical output of typical high-power
LEDs to the lens. Again,
the reasons why larger F-numbers are less desirable for
transmit use are beyond the scope of this page - email me
for further information.
Because of its reasonably good quality and low price I would consider this to be an excellent lens for optical communications work - if you can find one like it! The folks in the UK, having built quite a few optical systems using these sorts of lenses, have had quite good luck and consistent results (as long as they used lenses with focal lengths in the 300-350mm range) indicating generally consistent quality across different brand names. I have also constructed some LED transmitters with these lenses and they have produced good, parallel beams.
|
Lens #4 - 3dlens.com Product #A260:
This is another optical acrylic lens sold by 3dlens.com and is 260mm x 260mm with a focal length of 200mm with a groove pitch of 0.2mm and a thickness of about 2mm.
This lens also has a nicely-controlled blur circle and a fairly short F-number of 0.77. When used for transmitting, a square lens is somewhat more efficient than a rectangular one because less of the circular light projected from the source is cut off along the edges.
The F-number of this lens is quite low, but it is perfectly usable. The only downside of this lens is that the groove pitch is 0.2mm, which slightly increases scattering losses.
 |
Lens #5 - 3dlens.com Product # A395b:
This is yet another lens from 3dlens.com and 395mm x 395mm, with a focal length of 220mm, a groove pitch of 0.5mm and is constructed of 2mm thick optical acrylic. As can be seen from figure 5, this lens also produces a reasonably good-quality spot.
The F-number of this lens (0.57) is low, making it a bit of a challenge to use, but it can offer excellent results with proper techniques.
For some reason this lens has rounded corners - a factor that slightly complicates its mounting in a frame as those corners would allow dust to enter and air to pass through - although it would be pretty easy to seal the corners with plastic or cardboard or (carefully!) cut it down to a smaller, square-cornered size which would also effectively increase the F-number. As with lens #4, because this lens is square there will be lower transmission losses from vignetting of the round pool of light along the edges than would be the case with a rectangular lens.
|
Lens #6 - Anchor Optics P/N: AX27363:
This unusual-looking lens is round, with an active area of about 335mm in diameter with a groove pitch of about 0.5mm. This lens appears to be on its original factory "blank" - that is, it would seem to have been intended that a square lens of 285mm per side (with an "active" area of 270mm, square, bounded by a border that is about 8mm wide) be cut from it. The focal length is approximately 230mm.
This lens appears to be of good quality and as can be seen from Figure 10, it produces a nice, tight pattern. In the image I managed to catch a little bit of coma due to a slight misalignment, although that is not an intrinsic property of the lens.
This lens is apparently a surplus item sold by Anchor Optics - but they seem to have a reasonable supply of them as it shows up frequently on various optical-related forums. Interestingly, the online catalog lists this lens as having a 15 inch (381mm) focal length - but the samples that I have are definitely closer to 230mm! I'm not sure if they mis-measured the focal length, or if there are a number of the same-sized lenses in their stack with different focal lengths!
With an F-number ranging from 0.69 (if you consider the diameter of the grooved section ) to 0.85 (if you only consider the "square" section) it has a fairly short - but useful - ratio. The coarse grooves minimize scattering losses making it a reasonable lens for both transmission and reception. Because of it's square/round shape, optical transmission systems constructed using it are more efficient as a smaller amount of the circle of light from the LED is truncated along the edges than would be the case with a rectangular lens.
I would consider this to be an excellent lens for optical communications work.
Important comment about surplus Fresnel lenses: As is occasionally the case with surplus Fresnels, different focal-length lenses may be mixed together - particularly if they have similar physical dimensions and do not appear, at first glance, to differ from each other. Such may be the case with some of the lenses from Anchor Optics: As noted above, the catalog stated that this lens had a focal length of 381mm but my sample was closer to 230mm - and the observation that the lenses received differ from the catalog specifications has been reported to me by at least one other person!
 |
Lens #7 - Anchor Optics P/N: AX70877:
Not all Fresnel lenses are created equal - which is to say that not all of them are made for the same purpose. This lens - the Anchor Optics AX70877 - was apparently made for Overhead Projector use or as some sort of large condenser lens. It is common, with these types of lenses, that they not be designed to focus at infinity which means that one shouldn't be surprised to see that they perform poorly when called on to do so!
This lens is 283mm square (with cut-off corners) with an active area of about 265mm square with a groove pitch of between 0.35 and 0.5mm and about 2mm thick. The focal length - when one attempts to focus it at infinity - is around 390mm, but since it does not focus well at all this measurement is only approximate. Made by a company called "Cryton Optics Inc." of Roslyn, N.J. it appears to be of good quality - but just not the sort of thing you would use for focusing anything at infinity - or even 15 meters!
As is seen in Figure 11, this lens produces a fairly large spot - but that's not the entire story: Much of the light focused onto the image was actually spread out over a far larger area than the imager and is below the its threshold of sensitivity - but clearly visible (and covering more than the entire face of the imager) when the LED current was turned up to maximum and the picture was enhanced (which brought up the noise considerably) to show the very dim details.
Lens #8 - Surplus Shed L3707 (610mm F.L.)
Some time after building a box to use lens #10 (below) I decided to order some spare lenses. Unfortunately, they were sold out - but they had one of these (610mm F.L.) lenses onhand, so I decided to get it anyway out of curiosity. When it arrived I could see that it was of the same, high quality as the identically-sized lenses (#10) - just a different focal length.
Even though the F-number is a somewhat long (but reasonable) 1.42, this focal length would imply that the box or mechanical assembly used to hold the lens and electronics would be quite large. Properly "illuminating" this lens with an LED would be a bit of a challenge, but it would make a nice lens for a receiver - provided that the photodetector was large enough: A BPW34 would work nicely!
 |
Lens #9 - 3dlens.com Product # 406f:
This is another of the "Page Magnifier" lenses - but instead of optical acrylic it is made from much thinner (approx. 0.4mm) clear, flexible vinyl with a groove pitch of 0.3mm.
This particular lens includes a "frame" of black, flexible vinyl to permit mounting in a 3-ring binder and to allow handling without touching the lens area and is about 194mm x 270mm (with a 35mm long "handle) and a lens area of 158mm x 222mm. Because this lens is flexible, it is necessary to hold it flat (against, or sandwiched between pane(s) of glass or acrylic) in order for it to focus properly.
As can be seen from Figure 13 this lens would appear to have comparatively high scattering losses, but considering its intended purpose this is not too surprising! Admittedly, during this test I may not have held the lens as "flat" as it should have been so it's on my list of lenses to re-test some time in the future.
|
Lens #10 - Surplus Shed L3606 (330mm F.L.)
When I ordered lens #2, it was intended to be a spare for this lens, but as mentioned, it wasn't of the same focal length as this one!
This lens was obtained from SurplusShed.com (P/N: L3606) and is 250mm x 318mm and is about 2mm thick with a focal length of 330mm and a groove pitch of about 0.5mm. (As you have probably guessed, the stock of this surplus lens has been depleted.)
As can be seen from Figure 14, this lens produces a very "tight" spot of light - arguably better than any of the other lenses tested. Due to a variation in the setup the image in this figure is somewhat darker than those above.
Lenses of this type were used in my First Optical Transceiver.
 |
Lens #11 - Surplus Shed L3707 (229mm F.L.)
This is the lens for which lens #8 was ordered as a spare, but the Focal Length was different.
The story gets rather complicated at this point: On the Surplus Shed web page this lens had originally been listed as having a 24 inch (610mm) focal length, but when I got them, I saw that they were around 229mm (approx. 9 inches.) This turned out for the better as the 9" focal length - although a bit short of an F-number - made for a rather compact enclosure for a lens of this size while the originally-stated focal length (610mm) would have required quite a large box! Now, before anyone gets the idea that the folks at Surplus Shed didn't have their act together, it should be pointed out that they weren't aware that these identically-sized Fresnels seemed to have come in different focal lengths until someone (not me!) pointed it out. By the time they realized this (and changed their on-line catalog) they had more-or-less depleted the stock of lenses for which I desired spares.
Anyway, this lens, like #8, is 404mm x 430mm and 2mm thick with a 0.5mm groove pitch. Unlike that lens, this one has a 229mm focal length, meaning that it has an F-number of 0.53 - shorter than that of lens #5. As can be seen in Figure 15 this lens produces a nice, tight spot of light. As with lens #10, a variation in the setup resulted in a somewhat darker image than many of the above images.
The short focal length of this lens makes its use slightly awkward, but I have very successfully use a pair of these lenses in my "Foldable" optical transceiver.
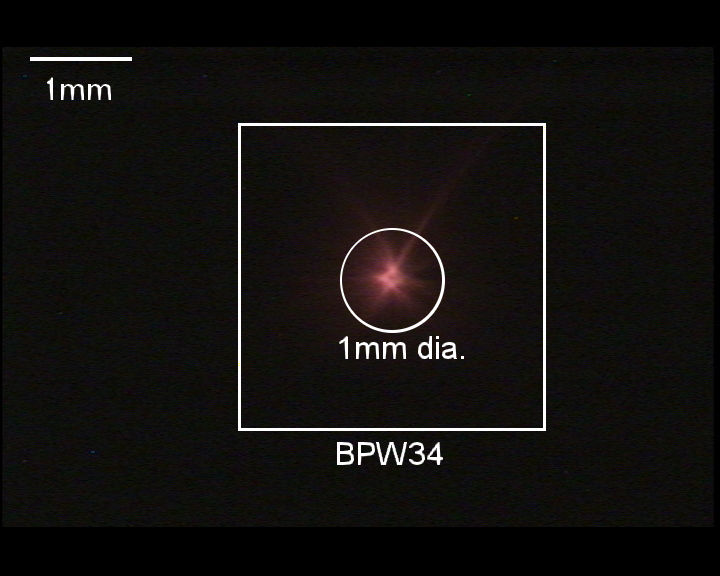
Annotated picture showing typical detector sizes:
|
For comparison, Figure 16 shows the blur circle size of lens #3 (the "Page Magnifier" lens) and some typical detectors.
The larger square depicts the size of a BPW34 photodiode, a diode that has an area of 7.5mm2 and is inexpensive (well under $2 U.S. in small quantities) and a reasonably good performer in terms of leakage currents and intrinsic noise. Its moderate size means that its capacitance is quite reasonable (70pF at 0 volts, 25pF at 3 volts and just 10pF at 20 volts of reverse bias) and is large enough to be able to "capture" pretty much all of the of light focused by the lenses described on this page.
Also represented is the relative size of a hypothetical 1mm diameter photodiode. A diode of this size has about 1/10th the area of a BPW34 which will have comparatively lower capacitance (because of its lower area) as well as lower intrinsic noise and such a diode would be capable of capturing the vast majority of the light focused by this lens. Even though some of the light would "spill" past a diode of this size, it's likely that, compared to the BPW34, one would achieve somewhat higher performance with it owing to the lower capacitance of the diode and lower noise contribution. If other light sources are nearby, the narrower field of view of this diode/lens combination (as compared with the same lens using the BPW34) may provide additional performance gain by helping reject off-axis sources that might otherwise "dilute" the desired signals.
Conclusions:
It's rather difficult to estimate the size of the "blur circles" of the lenses tested above but it is very clear that the blur circles are very much larger than would be the airy discs at the tested wavelength, but let's take another look at the Figure 16 where we are testing lens #3. By inspection and "guesstimation" we'll declare that the diameter of the blur circle (where the vast majority of the spot is contained) is, in round numbers, on the order of 0.2mm. In looking at Table 1 (above) we see that for an F-number of 1.25 (very close to the measured F-number of this lens) that the diameter of the airy disc would be just under 1/1000th of a millimeter - approximately a 200-fold difference!
So, we can see that neither this Fresnel lens - or any of the others on this page - come anywhere near the the diffraction limit!
Comment:
As a rough estimate and as a rule of thumb, the diameter of the "blur circle" of a good quality, molded plastic Fresnel lens is approximatly 1/1000th of the focal length of the lens. It has also been observed that some very high-quality lenses have 1/2-1/3 this size of blur circle.
Implications for "transmitting":
Given that the area of a typical, high-power LED (such as one of the members of the Luxeon or Cree family) are at least 1mm2 in size, we can be reasonably assured that, for the majority of the lenses described above (particularly those that have an F-number below about 1.5) that even after a moderate amount of source-size magnification by a secondary lens, the divergence of the resulting collimated beam will be largely set by the size of the emitter and not the quality of the lens.
Given a "typical", inexpensive Fresnel lens of "Page Magnifier" size with a 300mm focal length, knowing the size of the "blur circle" for such a lens implies that with a small emitter (that is, one that is about the same size as the blur circle) that one could achieve somewhere in the general area of 0.05 degrees (about 0.9 milliradians) of beam divergence. Considering that the brightest LEDs (e,g, that is, those that have the highest "current density" - number of amps per square millimeter and thus the highest photonic density) are much larger than the blur circle, achieving that degree of divergence is unlikely - unless one were to mask off a larger emitter and "throw away" the extra light!
The penalty of using a "larger than necessary" emitter is mostly one of inconvenience in that more power is required to light up the "unused" portion of the LED's emitting area, plus the fact that the actual beamwidth tends to be broader - which has implications when it comes to using a full-duplex optical communications system and Rayleigh scattering increasing transmit-receive crosstalk. On the positive side, a broader beam makes aiming much easier and relaxes the mechanical precision requirements of the emitter/lens assembly!
Implications for detectors:
As with the emitter, a detector of 1mm diameter (or larger) is more than adequate to intercept the vast majority of energy being focused by the lens tested above to its focal plane. Detectors much smaller than this (depending on the lens, of course) run the risk of not intercepting as much of the distant source's energy, resulting in loss of efficiency. The use of a detector that is much larger than the blur circle could introduce inefficiency due to the capacitance and noise of the photodiode degrading the signal from it as well as the larger size increasing the field of view of the system.
All of this assumes that the detector is situated precisely at the focal plane of the lens and that it can be held there with good accuracy, despite transportation and handling! With these (or any!) lenses it is important that sub-millimeter accuracy and stability be maintained in the structures in order to keep the components in proper focus and paraxial alignment!
Final comments:
Hopefully, this page gives a general idea of what can be expected from typical, molded plastic Fresnel lenses. Again, this information can be useful in determining reasonable sizes of detectors - or, as in the case of a Photomultiplier tube which has a much larger "active area", a reasonable size of aperture that might located at the focal plane to limit the field of view. This information also gives an idea as to what might be the limiting factor when it comes to minimizing divergence for this type of Fresnel lens - that is, lens accuracy/quality or the apparent size of the emitter.
Return to the KA7OEI Optical communications Index page.
If you have questions or comments concerning the contents of this page, or are interested in this circuit, feel free to contact me using the information at this URL.
Keywords: laser pointer, laser, pointer, Lightbeam communications, light beam, lightbeam, laser beam, modulated light, optical communications, through-the-air optical communications, FSO communications, Free-Space Optical communications, LED communications, laser communications, LED, laser, laser voice, laser voice transmitter, laser voice communicator, laser communicator, laser transmitter, laser voice sender, laser pointer transmitter, laser pointer transceiver, laser pointer communicator, laser pointer communications, laser pointer voice communicator, laser pointer voice communications, light-emitting diode, lens, fresnel, fresnel lens, photodiode, photomultiplier, PMT, phototransistor, laser tube, laser diode, high power LED, luxeon, cree, phlatlight, lumileds, modulator, detector
This page and contents
copyright 2009-2015. Last update: 20150820